Muestras de fórmulas matemáticas en HTML
Clases del módulo Math

En este tema veremos las clases del módulo Math que nos permiten escribir HTML y CSS suficiente para presentar visualmente una fórmula matemática. Y, adicionalmente, poder extraerla como una expresión en lenguaje natural válida para usarla en aplicaciones como Wolfram Alpha.
En la Figura puede ver como presentamos la raíz cuadrada usando el símbolo UNICODE "√". El estilo en forma de clases con un guion bajo inicial y dos letras aplicarán lo necesario para incluir la línea superior que abarca la raíz, algo que el simple caracter "√" no incluye. En lenguaje natural la extraemos como sqrt(n), expresión que podemos usar en Wolfram Alpha y otras aplicaciones. Empecemos por listar las clases disponibles con la versión actual.
Versión 2023-07-08_21-40
_al⇒text-align:left_ar⇒text-align:right_bb⇒border-bottom:currentColor solid 0.0625em_bc⇒border-color:[string]⇒/^_bc([a-z]+)$/_bg⇒background-color:[string]⇒/^_bg([a-z]+)$/_bl⇒border-left:currentColor solid 0.0625em_bn⇒border:none_bo⇒border:currentColor solid 0.0625em_br⇒border-right:currentColor solid 0.0625em_bs⇒border-spacing:[number/100 em]⇒/^_bs(\-?\d{1,3})$/_bt⇒border-top:currentColor solid 0.0625em_bw⇒border-width:[number/100 em]⇒/^_bw(\-?\d{1,3})$/_by⇒border-style:[string]⇒/^_by([a-z]+)$/_co⇒color:[string]⇒/^_co([a-z]+)$/_di⇒display:inline_dn⇒display:inline-block_do⇒display:none_ff⇒font-family:[string]⇒/^_ff([a-z]+(?:S[a-z]+)*)$/_fn⇒font-style:normal_fs⇒font-size:[number/100 em]⇒/^_fs(\-?\d{1,3})$/_fw⇒font-weight:bold_he⇒height:[number/100 em]⇒/^_he(\-?\d{1,3})$/_lh⇒line-height:[number/100 em]⇒/^_lh(\-?\d{1,3})$/_ma⇒margin:[number/100 em]⇒/^_ma(\-?\d{1,3})$/_mb⇒margin-bottom:[number/100 em]⇒/^_mb(\-?\d{1,3})$/_ml⇒margin-left:[number/100 em]⇒/^_ml(\-?\d{1,3})$/_mr⇒margin-right:[number/100 em]⇒/^_mr(\-?\d{1,3})$/_mt⇒margin-top:[number/100 em]⇒/^_mt(\-?\d{1,3})$/_nu⇒visibility:visible_ol⇒text-decoration:overline_ou⇒outline:currentColor dotted 1px_pa⇒padding:[number/100 em]⇒/^_pa(\-?\d{1,3})$/_pb⇒padding-bottom:[number/100 em]⇒/^_pb(\-?\d{1,3})$/_pl⇒padding-left:[number/100 em]⇒/^_pl(\-?\d{1,3})$/_pr⇒padding-right:[number/100 em]⇒/^_pr(\-?\d{1,3})$/_pt⇒padding-top:[number/100 em]⇒/^_pt(\-?\d{1,3})$/_ul⇒text-decoration:underline_va⇒vertical-align:middle_vb⇒vertical-align:bottom_vc⇒vertical-align:center_ve⇒vertical-align:[number/1 %]⇒/^_ve(\-?\d{1,3})$/_vi⇒visibility:hidden_vs⇒vertical-align:baseline_vt⇒vertical-align:top_wi⇒width:[number/100 em]⇒/^_wi(\-?\d{1,3})$/_ws⇒white-space:pre_xa⇒Factorial ascendente o Pochhammer_xb⇒Binomial_xc⇒Definición función a trozos (Piecewise)_xd⇒Factorial descendente_xg⇒Grupos en fracciones de nivel 4_xh⇒Separador fracción_xi⇒Infinito complejo_xm⇒Matrices_xn⇒Caracteres multilínea
Preferiblemente usaremos un DIV, SPAN o TABLE para dotarle de la clase math, dentro de cuyo elemento escribiremos la fórmula, cabiendo usar elementos I para dotar de estilo a partes internas. Para la visualización no hay limitación en el uso de elementos HTML, pero para la funcionalidad de Copy Math que veremos después, se limitan los elementos y atributos que pueden contener con este código en copy-math.js:
let tagsAllow = ["div", "span", "i", "table", "tr", "td", "th",
"sub", "sup"];
let attrsAllow = ["rowspan", "colspan", "class", "style"];Esto quiere decir que cuando exportemos a HTML la fórmula en Copy Math cualquier cosa que no sea eso será ignorado o bien acusará error no permitiendo exportar. Por ejemplo, la siguiente fórmula tiene el HTML <div class="math">x + <b>y</b></div>, de tal forma que se visualizará correctamente pero al obtener el HTML nos devolverá "Elementos no permitidos : b":
Los atributos no permitidos serán ignorados, como este que tiene <div class="math">x + <i class="_cored" title="y">y</i></div> donde se ignora el atributo title al exportar a HTML:
Las clases de la lista son de la forma _[a-z]{2}, empezando con un guion bajo y dos letras. Por ejemplo, con la clase _bt que presenta un borde superior (border-top):
<div class="math">y = <i class="_bt">x<sup>2</sup>+1</i></div>
Verá que en la lista anterior aparece la entrada _bt definiéndola como border-top: currentColor solid 0.0625em. Son clases que aportan un estilo particular fijo, no modificable. Otras clases permiten modificar el estilo. Si queremos dotar de color y más grueso a ese borde superior, usaremos las clases _bc (border-color) y _bw (border-width):
<div class="math"> y = <i class="_bt _bcred _bw20">x<sup>2</sup>+1</i> </div>
Estas son las clases que presentan estilos en línea con el elemento mediante la ejecución de la función applyView() del módulo Math. Por ejemplo, con _bcred aplicamos style="color: red", con _bw20 aplicamos style="border-width: 0.2em". Vea que en este caso pasamos 2 dígitos y se divide entre 100, agregando a continuacion "em", que es lo que significa [number/100 em] en la lista anterior para estas entradas. Finalmente mediante la función applyView() lo que se renderiza en el navegador es lo siguiente:
<div class="math"> y = <i class="_bt _bcred _bw20" style="border-color: red; border-width: 0.2em;">x<sup>2</sup>+1</i> </div>
Para las clases modificables se acompaña el patrón de expresión regular para ver como podemos escribirla. Por ejemplo, para el borde superior que vimos antes el patrón es /^_bc([a-z]+)$/, lo que supone que es _bc seguido de una o más letras en minúscula. Para el grueso del borde tenemos el patrón /^_bw(\-?\d{1,3})$/, que supone pasar _bw, opcionalmente un guion que significa número negativo, y después de 1 a 3 dígitos.
En algún caso es necesario escribir espacios, como para la clase _ff que permite configurar la fuente (font-family). El patrón es /^_ff([a-z]+(?:S[a-z]+)*)$/, significando una o más letras minúsculas seguido, opcionalmente, de un "S" mayúscula y una o más letras minúsculas. La "S" significa espacio, así que para pasar el estilo style="font-family: \"Arial Black\"" pasaremos la clase _ffarialSblack. No confundir la "S" literal con la escapada "\S" que en expresiones regulares significa cualquier caracter que no sea un espacio.
Usamos dos letras para identificar la clase, en la medida de lo posible que se pueda identificar con la propiedad, como _bc para border-color, tomando una letra de cada palabra. Por supuesto que no puede trasladarse todo el CSS a claves de dos letras, pero tampoco necesitaremos usar más estilo CSS que el suficiente para presentar adecuadamente una fórmula matemática.
Las clases en color azul son las que definen estructuras o fórmulas concretas. Pueden aplicar estilo, como la clase _xn que se utiliza para ajustar los caracteres multílinea. Pero en la mayoría su función principal es que el módulo Copy Math pueda reconocer la expresión en lenguaje natural que debe extraer. He reservado las clases a partir de la letra "x" para esto. Por ejemplo, _xb define el binomial:
Extrayendo en lenguaje natural obtenemos la expresión C(n, k), fórmula reconocida para el binomial o combinaciones. El HTML escrito es el siguiente:
<div class="math">
<i class="_xb _fs200">(<i>n</i><i class="_ml-60">k</i>)</i>
</div>Y el finalmente presentado en esta página es el siguiente, aplicándose estilo en linea para las clases _fs200 y _ml-60:
<div class="math">
<i class="_xb _fs200" style="font-size: 2em;">(<i>n</i><i class="_ml-60" style="margin-left: -0.6em;">k</i>)</i>
</div>En esta página ponemos más ejemplos sobre estas clases estructurales. Usando Copy Math puede observar el HTML para ver como están escritas.
Tras exponer lo anterior se comprende que para escribir fórmulas matemáticas directamente en HTML, es necesario saber como se comporta HTML y el CSS que se le aplique. Podríamos hacer un editor que permitiera al usuario escribir fórmulas matemáticas sin saber HTML y CSS, pero esa es otra historia.
Exportar recursos para usar en la web
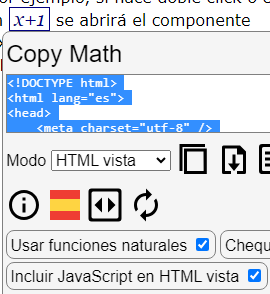
Como explicamos en unos apartados del tema anterior sobre la configuración de Copy Math, puede exportar el HTML+CSS+JavaScript para insertarlo en una página web. Por ejemplo, si hace doble click o copia esta expresión x+1 se abrirá el componente permitiendo exportar a la vista HTML, tal como se observa en la Figura.
En la configuración hay que marcar la opción incluir JavaScript en HTML. El código contiene todo el HTML, CSS y JavaScript para que funcione en una página web aparte, sin más recursos.
El código resumiendo partes con puntos suspensivos para verlo en su totalidad es el siguiente:
<!DOCTYPE html>
<html lang="es">
<head>
<meta charset="utf-8" />
<meta name="viewport" content="width=device-width, initial-scale=1" />
<title>Copy Math</title>
<style id="css-math">
...
.math._al,.math *._al{
text-align:left;
}
.math._ar, .math *._ar {
text-align: right;
}
...
</style>
<script defer>
var myApplyView = (function (){
styles = {
_bg:{prop:"background-color",reg:/^_bg([a-z]+)$/,type:"string"},
_bc:{prop:"border-color",reg:/^_bc([a-z]+)$/,type:"string"},
...
};
function applyViewShort() {
...
}
return applyViewShort;
})();
window.setTimeout(myApplyView);
</script>
</head>
<body>
<div style="margin:0.5em">
<span class="math _bo _pl20 _pr20">x+1</span>
</div>
</body>
</html>Se observa el CSS con las clases con estilo fijo. Y el JavaScript con la función applyViewShort() que aplica el estilo de las clases configurables cuando se cargue el script diferido. Bien puede usar esta técnica o cualquier otra, pues en cualquier caso esa es la función que se encarga de esa tarea.
Símbolos matemáticos en UNICODE
UNICODE ofrece un conjunto de símbolos matemáticos que nos permiten presentar las fórmulas. Hay muchos sitios con esta información. Este par de enlaces son una muestra:
En lo siguiente se agrupan los más significativos:
- Operadores: + - * × / ÷ ^ ∑ ∏ ± ∓
- Raíces: √ ∛ ∜
- Fracciones: ½ ⅓ ¼ ⅕ ⅙ ⅐ ⅛ ⅑ ⅒ ⅔ ⅖ ¾ ⅗ ⅜ ⅘ ⅚ ⅝ ⅞ ⅟
- Lógicos: ∧ ∨ ⊻ ⊼ ⊽ ∀ ∃ ∄ ∈ ∉ ⊂ ⊄ ∩ ∪ ⋀ ⋁ ⋂ ⋃
- Comparativos: < > = ≠ ≤ ≥ ≰ ≱ ⪇ ⪈ ≦ ≧ ≨ ≩
- Aproximaciones: ~ ≁ ≈ ≉ ≂ ≃ ≄ ≅ ≆ ≇
- Paréntesis: ( ) ⟮ ⟯( )❨ ❩ ❪ ❫﹙﹚⁽ ⁾ ₍ ₎
- Corchetes: [ ][ ]﹝﹞
- Redondeos: | | ⌈ ⌉ ⌊ ⌋
- Llaves: { }{ }❴ ❵﹛﹜
- Flechas: ⇐ ⇒ ⇔ ← → ↔ ⟵ ⟶ 🠐 🠒 🡐 🡒 ⭠ ⭢ ⭤
- Varios: ∞ π ∅ Γ ∂ ∫ ∬ ∭ ∮ ∯ ≡ ≢ ≝ ℕ ℤ ℚ ℝ ℂ Ω ℧
- Griego: Γ Δ Θ Λ Ξ Π Σ Φ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω
- Superíndices: ⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁱ ⁿ ⁺ ⁻ ⁼ ⁽ ⁾
- Subíndices: ₀ ₁ ₂ ₃ ₄ ₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ₐ ₑ ₒ ₓ ₔ ₕ ₖ ₗ ₘ ₙ ₚ ₛ ₜ
En principio la representación visual de estos símbolos debería ser la misma en todos los navegadores. Pero no siempre es así, como explicamos en el apartado de símbolos multilínea. Esta técnica de usar UNICODE y elementos TABLE, DIV, SPAN e I para presentar fórmulas matemáticas puede simplificar las cosas. Pero la desventaja es que dependemos de la visualización UNICODE.
Operadores
Los operadores básicos son
Hay que tener en cuenta que podemos escribir estos operadores en lenguaje natural y Wolfram Alpha los entenderá. Por ejemplo, el símbolo para el producto o la división admiten alternativas * × para el producto y / ÷ para la división:
Puede resolver ese cálculo usando el botón en Copy Math, obteniéndose 13. Tenga en cuenta el orden de prioridad de los operadores que da lugar a la precedencia de las operaciones: (), ^, *, /, -, +. Esto quiere decir que primero se resuelve lo que está en paréntesis, después la exponenciación, producto, división, resta y finalmente, la suma.Realmente el producto y la división son del mismo orden pues la división puede reducirse al producto con a/b = a*(1/b). E igual pasa con la resta que puede reducirse a una suma, pues a-b = a+(-b). Por estas cosas en la expresión anterior podemos prescindir de los paréntesis implícitos, pues el orden de precedencia equivale a ponerlo con paréntesis, siendo estas tres expresiones equivalentes:
Siguiendo el orden de precedencia, con o sin usar paréntesis, se resolvería en estos pasos:
O bien:
Para cambiar el orden de precedencia por defecto hemos de poner los paréntesis en otros sitios, obteniéndose en este caso el resultado 21 para este ejemplo:
Y este el el órden de cálculo, resolviendo primero los paréntesis:
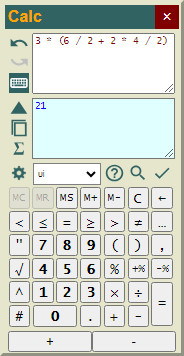
Sin embargo una aplicación como la Calculadora no realiza los cálculos así, dado que la gestión de paréntesis no es muy eficiente. Expliquemos un poco esto. Una expresión matemática infija es algo como "1 + 2", mientras que su transformación en RPN (Notación Polaca Inversa o Reverse Polish Notation) es "1 2 +". En esta notación el operador le sigue a dos operandos, mientras que en infija el operador está entre los dos operandos. La notacion RPN es más cómoda para calcular en un programa porque se prescinden de los paréntesis. La transformación infijo-RPN y el posterior cálculo del RPN se realizan ambos usando pilas. La transformación infijo a RPN se consigue con el algoritmo de shuting yard inventado por Dijkstra.
El módulo Calc (Calculadora) realiza los calculos convirtiendo la expresión en una lista (pila) RPN. De hecho en la calculadora hay una función para obtener el RPN de una expresión. Si pasamos rpn("3 * 6 / 2 + 2 * 4 / 2") obtenemos la lista "3, 6, *, 2, /, 2, 4, *, 2, /, +". Una vez se obtenga esa lista el módulo Calc procede a calcularla de izquierda a derecha de tal forma que cuando encuentre un operador realizará esa operación con los dos operandos anteriores en la lista. Si lo aplicamos a ese RPN este sería el cálculo:
3, 6, *, 2, /, 2, 4, *, 2, /, + 18, 2, /, 2, 4, *, 2, /, + 9, 2, 4, *, 2, /, + 9, 8, 2, /, + 9, 4, + 13
En cambio para la segunda expresión obtenemos rpn("3 * (6 / 2 + 2 * 4 / 2)") obtenemos "3, 6, 2, /, 2, 4, *, 2, /, +, *" y su cálculo es:
3, 6, 2, /, 2, 4, *, 2, /, +, * 3, 3, 2, 4, *, 2, /, +, * 3, 3, 8, 2, /, +, * 3, 3, 4, +, * 3, 7, * 21
El operador producto no es necesario especificarlo si no hay duda. Por ejemplo, estas cuatro expresiones son válidamente evaluadas por Wolfram Alpha:
Wolfram Alpha entiende como variables las letras individuales. Así "x" e "y" son variables y, por tanto, entre ellas y el "2" insertará operadores producto. Explicamos todo lo anterior porque cuando escribimos expresiones, o bien cuando Copy Math la extrae en lenguaje natural, puede prescindir de paréntesis innecesarios o de operadores producto. Por ejemplo con esta fracción que luego veremos en otro apartado:
| f(x) = | a+b | x |
| c+d | y |
Al extraer la expresión en lenguaje natural resultará:
f(x) = (a + b) / (c + d)(x) / (y)Podría parecer que no es correcta. Pero lo primero es ver que parece que falta el operador producto que se entiende implícito. Y además podríamos añadir paréntesis y eliminar algunos innecesarios. Quizás así se vea mejor, pero no es necesario pues la expresión anterior es válida:
f(x) = ((a + b) / (c + d)) * (x / y)Los términos como (x) e (y) son extraidos en Copy Math con paréntesis aparentemente innecesarios. Podría eliminarlos en el código que ejecuta Copy Math, pero se me presentan posibles confusiones como el caso de f(x) en la fórmula anterior: ¿podría entenderse la "f" como una variable siendo f(x) = f*(x) = f*x en lugar de lo que queremos expresar como una función? Wolfram Alpha entiende que f(x) es una función. Por otro lado (f)(x) es un producto de dos variables "f" y "x", como si fuera f x prescindiendo del operador producto. O incluso como fx si entendemos que las variables son letras individuales y que entre ellas, aunque no haya espacios, está implícito el producto.
Por estos motivos he decidido que términos individuales como (x) e (y), e incluso dígitos como (2), puedan aparecer con paréntesis. Asi cuando encontremos algo como w(x) entonces "w" será una función y no una variable y no eliminaremos los paréntesis pues desvirtuaría su significado, pues pasaría a ser w*x. Como ejemplo, compruebe las siguientes expresiones que se obtienen en lenguaje natural y como Wolfram Alpha las evalúa, la primera como una función y la segunda como un producto:
Los operadores ± ∓ han de ser extraidos en lenguaje natural en dos partes:
Para la primera la expresión obtenida es 4 + 2, 4 - 2, en dos partes separadas por una coma, obteniéndose una pareja alternativa de resultados 6, 2 separados por coma. Recuerde que en el módulo Calc la coma separa listas, no decimales, pues se usa el punto para separar decimales. La segunda se obtiene lo mismo al revés.
El operarador "^" se usa para la exponenciación, por ejemplo 42 usa el elemento SUP <span class="math">4<sup>2</sup></span>, cuya expresión en lenguaje natural es 4^2. Este operador exponenciación es de uso común, reconociéndolo Wolfram Alpha. JavaScript en cambio no lo usa, ejecutándose la exponenciación con Math.pow(4, 2) o bien con 4**2. Wolfram Alpha y Calc reconocen las tres 4^2, pow(4, 2), 4**2.
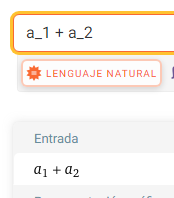
El elemento SUP es un superíndice que funciona como un operador. Mientras que SUB es para subíndice, pero no es un operador. Por ejemplo a1 + a2 cuya expresión es a_1 + a_2. Wolfram Alpha reconoce los subíndices, como se observa en la Figura, pero sólo cuando tienen un valor numérico. Como las variables son letras individuales, es una forma de ampliar el conjunto de variables.
En Calc esto no tiene ninguna utilidad pues no es un operador, aunque más abajo veremos como usar "_" y "^" como índices de sumatorios y productos ∑ ∏, pues Calc es capaz de realizar estas sumas y productos con índices al menos de 100 mil posiciones.
Raíces
La raíz cuadrada es simple de hacer:
En el HTML usamos la clase _fs para dotar de tamaño de fuente font-size: 1.3em y así ajustar el símbolo "√" al borde superior, usando la clase _bt que agrega border-top: currentColor solid 0.0625em:
<div class="math"> <i class="_fs130">√</i><i class="_bt _ml12">n</i> </div>
Veamos otros ejemplos de raíces. Puede usar Copy Math para ver los detalles.
| f(x) = | √x3+2x2 |
| 1-x |
| f(x) = | √( | x2+1 | ) |
| 1-x |
| x = | -b ± √b2-4 a c |
| 2 a |
| Γ(x) = √( | 2π | ) ( ( | x | ) √( | x sinh( | 1 | ) + | 1 | ) ) x |
| x | e | x | 810 x6 | ||||||
Fracciones
Una expresión con una fracción en un término puede ponerse así, usando un elemento DIV:
Este es el código HTML escrito:
<div class="math">(a+b)/(c+d) + 1</div>
Pero visualmente es más legible usando un elemento TABLE:
| a+b | + 1 |
| c+d |
El HTML es este:
<table class="math">
<tr><td>a+b</td><td rowspan="3">+ 1</td></tr>
<tr><th></th></tr>
<tr><td>c+d</td></tr>
</table>El elemento TH sin contenido dibuja la línea de fracción. Observe el uso de rowspan para el término de la derecha por fuera de la fracción. Existe la clase estructural _xh (con un I vacío en su interior) que sobre un TD se comporta como TH, produciendo la misma presentación:
| a+b | + 1 |
| c+d |
<table class="math">
<tr><td>a+b</td><td rowspan="3">+ 1</td></tr>
<tr><td class="_xh"><i></i></td></tr>
<tr><td>c+d</td></tr>
</table>Sin embargo no debe usarse para separar fracciones de 2 niveles (numerador y denominador), pues no se reconoce al extraer la expresión en lenguaje natural. Esa clase _xh la reservaremos para fracciones de 4 niveles como veremos más abajo.
| f(x) = | a+b | + | x |
| c+d | y |
| f(x) = | a+b | * | x |
| c d | y |
| f(x) = | a+b | x |
| c+d | y |
| f 3(x) = | 6 |
| (1-x)4 |
| 1 | (z - x) = | 1 | z + z |
| x2 | x |
| G(x) = - | 1 | + | 2 |
| 1-x | 1-x-x2 |
| T(n) = | 2 | ( Φn+1 - δn+1 ) - 1 |
| √5 |
En los anteriores intervienen fracciones con 2 niveles: numerador y denominador. Si se requiren 4 niveles sería así:
| f(x, y) = | 1+x | + | y2 |
| xy | x | ||
| y+x | + | x2 | |
| y | 1-y | ||
La fórmula anterior tiene una línea de fracción central que el extractor de lenguaje natural identificará con la clase _xh con un elemento I vacío en su interior:
<tr><td colspan="3" class="_xh"><i></i></td></tr>
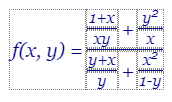
Las líneas de fracción en la parte superior e inferior seguirán siendo elementos TH vacios. En la Figura puede ver una imagen obtenida con Copy Math con la configuración bordes en celdas activada. Esto nos permite ver como se estructura la tabla, especialmente para visualizar el efecto de rowspan y colspan, como con este ejemplo. Observe que las lineas de fracción son celdas sin contenido, con altura cero, solo con un borde superior que se visualiza como una línea separadora de fracción. La línea de fracción central es la que contiene la clase _xh, con un colspan="3" para abarcar horizontalmente 3 celdas.
La expresión en lenguaje natural que se obtiene es la siguiente, donde se observa que la fracción central se indica con "÷" mientras que la superior e inferior con "/". Ambos operadores son reconocidos como división en lenguaje natural.
f(x, y) = ((1 + x) / (xy) + (y^2) / (x)) ÷ ((y + x) / (y) + (x^2) / (1 - y))La siguiente fórmula tiene un segundo término del numerador que no es una fracción:
| f(x, y) = | 1+x | + y2 | |
| xy | |||
| y+x | + | x2 | |
| y | 1-y | ||
El anterior tiene 1 grupo en el sentido de que tiene una única fracción global. El siguiente es de 4 niveles y 2 grupos de fracciones globales:
| f(x, y) = | 1+x | + y2 | w | ||
| xy | |||||
| + | |||||
| y+x | + | x2 | z2+3 | ||
| y | 1-y | ||||
En el HTML, que también puede ver en Copy Math, se puede observar que a partir del "+" y la fracción w/(z2+3) es un nuevo grupo de fracción global. Se identifica en el HTML con la clase estructural _xg y el número 1.
<table class="math">
<tr><td rowspan="7">f(x, y) =</td><td class="_fs80">1+x</td><td rowspan="3" colspan="2">+ y<sup>2</sup></td>
<td rowspan="3" class="_xg1"></td><td rowspan="3" class="_vb _xg1">w</td>
</tr>
<tr><th></th></tr>
<tr><td class="_fs80">xy</td></tr>
<tr><td colspan="3" class="_xh"><i></i></td><td class="_xg1">+</td><td class="_xg1 _xh"><i></i></td></tr>
<tr><td class="_fs80">y+x</td><td rowspan="3"> + </td><td class="_fs80">x<sup>2</sup></td>
<td rowspan="3" class="_xg1"></td><td rowspan="3" class="_xg1 _vt">z<sup>2</sup>+3</td>
</tr>
<tr><th></th><th></th></tr>
<tr><td class="_fs80">y</td><td class="_fs80">1-y</td></tr>
</table>Veamos ahora 4 niveles y 2 grupos, con fracción en el denominador del segundo, en color rojo:
| f(x, y) = | 1+x | + y2 | w | ||
| xy | |||||
| + | |||||
| y+x | + | x2 | z2+3 | ||
| y | 1-y | 2 x | |||
4 niveles y 3 grupos con fracciones en numerador y denominador del último grupo:
| f(x, y) = | 1+x | + y2 | w | xn + 1 | |||
| xy | y-1 | ||||||
| + | - | ||||||
| y+x | + | x2 | z2+3 | z3+x | |||
| y | 1-y | x-y | |||||
4 niveles y 3 grupos:
| f(x, y) = | 1+x | + y2 | w | Σn=0..∞ xn | |||
| xy | |||||||
| + | - | ||||||
| y+x | + | x2 | z2+3 | z3+x | |||
| y | 1-y | x-y | |||||
El siguiente con 4 niveles no tiene fracciones en los numeradores y encontramos una fracción en el denominador del último grupo:
| 1 | 1 | 1 | ||||
| = | × | |||||
| 1-x-xy | 1-x | 1 - | x | y | ||
| 1-x | ||||||
Otro de 4 niveles más complejo:
| (B | Ap | 1 | ||||||||
| - | ) ∫ | dx | ||||||||
| 2 | (x + | p | )2 + | (q - | p2 | ) | ||||
| 2 | 4 | |||||||||
Y otro más de 4 niveles:
| βn+1 | 1 | n! | 1 | |||
| (n+1)! | ||||||
| = | = | = | ||||
| βn | 1 | (n+1)! | n+1 | |||
| n! |
Las fracciones con 4 niveles no son muy usuales. Más niveles podrían ser posibles, pero no creo que merezca la pena el esfuerzo de programar su gestión, pues solo editarlas en HTML sería un verdadero lio.
Sumatorios, productos e integrales con índices
En lenguaje natural los caracteres "^" y "_" tiene un significado especial. Asi x^n es la exponenciación xn, que se presenta con el elemento SUP (superíndice):
<span class="math">x<sup>n</sup></span>
y x_n se reserva para los subíndices xn:
<span class="math">x<sub>n</sub></span>
Estos subíndices y superíndices asociados con ciertos símbolos matemáticos tienen también el cometido de definir el rango de un operador, como el sumatorio:
El HTML escrito es el siguiente, donde se observa que hemos desplazado hacia la izquierda con _ml-180 (margin-left: -1.8em) el elemento SUP para que quede alineado con el SUB:
<div class="math">
∑<sub>n=0</sub><sup class="_ml-180 _pr120">∞</sup> n
</div>Se extrae en lenguaje natural la expresión sum_(n = 0)^(∞) n, observando que primero ponemos lo que está en el elemento SUB y luego SUP.
A fin de simplificar el rango del sumatorio, en este sitio he adoptado el criterio de expresar alternativamente un rango como j ∈ [0, k] con la forma j=0..k, como el siguiente ejemplo del que se obtiene T(n, k) = 2 (sum_(j = 0)^k C(n, j)) - 1
El significado de los dos puntos seguidos para expresar un rango no es usual verlo. Sin embargo Wolfram Alpha reconoce estos 2 puntos (o 3) como la expresión de una progresión aritmética, puediendo comprobar que n=1..5 produce en Wolfram Alpha el resultado n = {1, 2, 3, 4, 5}, que es realmente lo que queremos expresar: un conjunto de números enteros desde el 1 hasta el 5 que se asignan a la variable "n".
Como parte de un sumatorio ∑n=1..5 n vemos que Wolfram Alpha produce el texto en lenguaje natural sum_(n=1)^5 n, cuya estructura con "_" y "^" es la que usamos en Copy Math. En cambio en lenguaje Wolfram se usa la expresión Sum[n, {n, 1, 5}], donde el rango es el segundo argumento {n, 1, 5}. En este lenguaje podemos usar incluso la notación de dos puntos escribiéndola como Sum[n, {n=1..5}], cuyo mismo resultado puede ver en este enlace directo a Wolfram Alpha.
Este es otro ejemplo con el rango n=0..∞ usando TABLE para presentar la fracción:
| A = ∑n=0..∞ xn = | 1 |
| 1-x |
Para simplificar más el rango n=0..∞ lo podemos poner como n≥0:
| B = ∑n≥0 xn = | 1 |
| 1-x |
Wolfram Alpha no soporta el rango n≥0 de forma directa, sino expresado con "_" y "^" como sum_(n = 0)^(∞) x^n y así lo exportamos en Copy Math. A continuación se presentan más ejemplos con formas distintas de ubicar los índices, pudiendo usar Copy Math para ver los detalles de cada una.
| B = ∑n=0∞ xn = | 1 |
| 1-x |
| D = Σn=0∞ xn = | 1 |
| 1-x |
| ∑n≥0 n | xn | = x ex |
| n! |
| ∑j=0..n | (n-j)k n! |
| (n-j)! |
Productos:
Integrales:
Límites:
En el módulo calc.js las sumas y productos en un rango se ejecutan con las operaciones sumi() y multi(). Por ejemplo,
| 1 + ( ∑n=1..5 | n2 | ) + | 8 |
| 2 | 3-5 |
El módulo Copy Math lo extrae como:
1 + (sum_(n = 1)^(5) n^2 / 2) + (8) / (3 - 5)Y el módulo Calc lo traduce a lo siguiente antes de ejecutarlo:
1 + (sumi("n", 1, 5, "n^2/2")) + (8/(3-5))Como se observan resaltados, el sumatorio debe contener paréntesis que la rodee a fin de determinar donde acaba la expresión del sumatorio, pues de otra forma todo lo que hay hasta el final formará parte del sumatorio. El rango no ha de sobrepasar 100000 posiciones. Lo mismo sucede con el producto:
| 1 + ( ∏n=1..5 | n2 | ) + | 8 |
| 2 | 3-5 |
Integrales y derivadas
Para la integral usamos el caracter ∫ que también reconoce Wolfram Alpha:
| ∫( | 1 | )dx |
| 1-x |
Hay caracteres multilínea para la integral:
Queda más estilizado, pero para extraer la expresión en lenguaje natural hay que incluir el caracter no multilínea "∫" y ocultarlo con la clase _do que aplica display: none, mientras que los multilínea hay que dotarlos de la clase _nu que viene a ser nulo a efectos de extraer la expresión, pero que no tiene ningún efecto CSS.
| ⌠ | ∫( | 1 | )dx |
| ⌡ | 1-x |
Para las derivadas usamos una fracción y los superíndices:
| d | ( | 1 | ) |
| dx | 1-x |
| d2 | ( | 1 | ) |
| dx2 | 1-x |
| d2 | ( | x | ) |
| dx dy | x-y |
| ∂2 | ( | y | ) |
| ∂x ∂y | x+y |
Todos son entendidos correctamente por Wolfram Alpha.
Combinatoria
La forma más simple de escribir un binomial es C(n, k) como una combinación, algo que Wolfram Alpha reconoce. Es mas díficil presentarlo visualmente de esta forma:
Usamos la clase estructural _xb para ayudar a Copy Math extraer la expresión C(n, k) en lenguaje natural:
<div class="math">
<i class="_xb _fs200">(<i>n</i><i class="_ml-60">k</i>)</i>
</div>Los dos argumentos del binomial los incluimos en elementos I. Hay que ajustar la posición del segundo elemento actuando con _ml (margin-left) y _pr (padding-right. Más ejemplos:
También podemos usar la clase estructural _xb para los números de Stirling de primera clase, que se traduce como abs(StirlingS1(n, k)) para que Wolfram Alpha pueda entenderlo:
Tiene el siguiente HTML:
<div class="math">
<i class="_xb _fs150 _lh110">[<i>n</i><i class="_ml-60">k</i>]</i>
</div>También puede usarse notación con "S" mayúscula S(n, k) = [nk] para los números sin signo devolviendo abs(StirlingS1(n, k)), usando "s" minúscula para los números con signo s(n, k) devolviendo StirlingS1(n, k), de tal forma que S(n, k) = abs(s(n, k))
Las permutaciones con repetición o multinomiales también pueden presentarse de esta forma alternativa:
Por ejemplo:
Podemos usar _ol con el estilo CSS overline y _ul con el estilo underline respectivamente para el factorial ascendente o Pochhammer y factorial descendente:
O bien usar bordes, _bt con el estilo CSS border-top y _bb con el estilo border-bottom:
Para extraer la expresión en lenguaje natural usaremos la clase estructural _xa y _xd para el ascendente y descendente respectivamente. Por ejemplo, para el primer caso se consigue encerrando en un elemento I con la clase _xa usando overline con _ol:
<i class="_xa">x<sup class="_ol">n</sup></i>
En lenguaje natural el factorial ascendente o Pochhammer se extrae como pochhammer(x, n). El descendente se extrae como factorialpower(x, n).
La siguiente tabla resume funciones combinatorias que el módulo Calc puede calcular con la columna "Expresión":
| Título | Math | Resultado | Expresión | Expresión compatible con Wolfram Alpha | Notas | |
|---|---|---|---|---|---|---|
| Combinaciones (Binomial) | (72) | 21 | C(7, 2) | ✓ | C(n, k) = n! / (k! (n-k)!) | |
| Combinaciones con repetición | ((72)) | 28 | CR(7, 2) | ✗ | C(7+2-1, 2) | CR(n, k) = C(n+k-1, k) |
| Permutaciones | P(7) | 5040 | P(7) | ✗ | P(7, 7) | P(n) = n! |
| Permutaciones | P(7, 7) | 5040 | P(7, 7) | ✓ | P(n, n) = P(n) = n! | |
| Permutaciones | P(7, 2) | 42 | P(7, 2) | ✓ | V(n, k) = P(n, k) = C(n, k) k! | |
| Permutaciones con repetición (Multinomial) | (74, 2, 1) | 105 | PR(4, 2, 1) | ✗ | multinomial(4, 2, 1) | PR(a, b, c, ...) = (a+b+c+...)! / (a!*b!*c!...) |
| Variaciones | V(7, 7) | 5040 | V(7, 7) | ✗ | P(7, 7) | V(n, n) = P(n, n) = n! |
| Variaciones | V(7, 2) | 42 | V(7, 7) | ✗ | P(7, 2) | V(n, k) = P(n, k) = C(n, k) k! |
| Variaciones con repetición | VR(7, 2) | 49 | VR(7, 2) | ✗ | 72 | VR(n, k) = nk |
| Factorial | 7! | 5040 | 7! | ✓ | n! = P(n) = P(n, n) | |
| Factorial doble | 7!! | 105 | 7!! | ✓ | n!! = n(n-2)(n-4)... | |
| Subfactorial | !7 | 1854 | !7 | ✓ | !n = [n!/e] | |
| Factorial ascendente (Pochhammer) | 72 | 56 | pochhammer(7, 2) | ✓ | nk = n!/(n-k)! | |
| Factorial descendente | 72 | 42 | factorialpower(7, 2) | ✓ | nk = (n+k-1)!/(n-1)! | |
En el módulo Calc el caracter "!" es el operador lógico para la negación, el mismo que se usa en JavaScript. Así que !true devolverá falso y !(5>4) también. Wolfram Alpha no reconoce este operador lógico, usando "!" para expresar factoriales y subfactoriales. He modificado el módulo Calc para cuando lo que antecede es un número entero entienda que es un factorial. Así 7! devuelve 5040. Y !7 es el subfactorial que devuelve 1854. Sin embargo dado que pueden haber confusiones con el signo "!", si la configuración "Usar funciones naturales" está marcada se traduce esta función:
- !7 =
subfactorial(7) - !n =
subfactorial(n) - n !(n-1) =
n subfactorial(n-1)
Es preferible traducirla siempre para no tener problemas de interpretación con Wolfram Alpha, por ejemplo.
Redondeos
Todo lo que esté entre dos barras verticales |...| se extrae en lenguaje natural como abs(...) para el valor absoluto. Si está con ⌈..⌉ se extrae como ceil(...) para el redondeo al entero superior. Y si está con ⌊...⌋ se extrae como floor(...) para el redondeo al entero inferior.
| A = | | | 1+x2 | | |
| 1-x |
| A = | ⌈ | 1+x2 | ⌉ |
| 1-x |
| A = | ⌊ | 1+x2 | ⌋ |
| 1-x |
Se pueden anidar
obteniéndose la expresión
y = ceil(z + abs(x^2 + floor(y - 1)))Matrices con caracteres multilínea

La facilidad de usar UNICODE para escribir fórmulas matemáticas es que tiene una gran cantidad de símbolos matemáticos. Pero la desventaja es que esos caracteres a veces no se visualizan exactamente igual en todos los navegadores. Depende en gran medida de la fuente elegida. En Math elegimos la fuente Georgia por tener un aspecto parecido a las fuentes que se usan para fórmulas matemáticas. Y además es soportada por la mayor parte de navegadores. Pero hay algunas diferencias.
En la Figura puede ver diferencias entre Chrome 114 (parte superior) y Firefox 115 (parte inferior). El símbolo UNICODE ∛ nos sirve para la raíz cúbica. Tal y como explicamos en el apartado de raíces, aplicamos Math para dibujar la línea superior de la raíz, probando valores y visualizándolo en Chrome, para lograr que la posición de esa línea superior sea la justa para que coincida con el símbolo de raíz. Al comprobarlo en Firefox vemos que se ajusta en vertical, pero no en horizontal. Esto es porque hay una leve diferencia entre la representación de ∛ en ambos navegadores. En navegadores de móviles el soporte UNICODE deja bastante que desear, observándose un comportamiento como el de Firefox. Navegadores basados en el motor Blink se comportan como Chrome, entre los que encontraremos Microsoft Edge, Opera, Brave y otros.
Los caracteres Unicode multilínea extienden su visualización mas arriba de la caja de línea. Sirven para agrupar varias líneas, como con las matrices. Y es aquí donde se observan más diferencias. En la Figura vemos un grupo de tres elementos de bloque con borde punteado apilados en vertical, de tal forma que representen tres líneas de texto. Los símbolos en color rojo { } son las llaves normales, viendo que en ambos navegadores ocupan una altura de línea normal. Los que siguen a continuación son los caracteres multílinea, visualizándose correctamente en Chrome ocupando entre 2 y 3 alturas de líneas. Pero en Firefox no se comportan así, y siguen ocupando una altura de línea.
A continuación se muestran en HTML los caracteres multílinea que podemos usar, teniendo en cuenta que su aspecto debe ser como el que aparece en la parte superior de la Figura. Si no es así no se asegura la correcta visualización de su uso en lo que vamos a ver en este apartado.
Para llaves de 2 líneas podemos usar estos:
Para corchetes podemos usar estos para la parte izquierda:
Y estos para la parte derecha:
La matriz más simple es un vector. En este caso usamos simplemente paréntesis y corchetes. Aunque con llaves también puede considerarse un vector, pues al menos Wolfram Alpha así lo reconoce:
Para los anteriores no es necesario un elemento TABLE. Usamos un DIV, aunque los elementos hay que separarlos con coma. Al extraer la expresión en lenguaje natural obtenemos V = (12, 5, 23), V = [12, 5, 23] o bien con llaves V = {12, 5, 23}. Para un vector columna si que es necesario un TABLE, donde cada fila es quién separa los elementos:
| V = | ⎧ | 12 | ⎫ |
| ⎪ | 33 | ⎪ | |
| ⎩ | 25 | ⎭ |
El HTML es el siguiente:
<table class="math"><tr><td rowspan="3">V = </td>
<td class="_xm">⎧</td><td>12</td><td class="_xm">⎫</td></tr>
<tr><td class="_xm">⎪</td><td>33</td><td class="_xm">⎪</td></tr>
<tr><td class="_xm">⎩</td><td>25</td><td class="_xm">⎭</td></tr>
</table>Al extraer la expresión en lenguaje natural obtenemos V = {{12},{33},{25}}. Para ello usamos la clase estructural _xm para encerrar las celdas con los paréntesis. Podríamos definir este ejemplo como un vector columna. Observe la diferencia con el vector fila. Cuando tiene más de una fila o columna la denominamos matriz:
| ⎧ | 2 | 15 | -7 | ⎫ |
| ⎪ | 33 | 6 | 10 | ⎪ |
| ⎩ | 25 | 8 | 13 | ⎭ |
De lo anterior se extrae {{2, 15, - 7},{33, 6, 10},{25, 8, 13}}, expresión en lenguaje natural que Wolfram Alpha entiende como una matriz. En lugar de números podemos incluir expresiones:
| ⎧ | x | x2 | x+y | ⎫ |
| ⎪ | 2x | x/y | (x+1)2 | ⎪ |
| ⎩ | x-y | 2π | √(n-1) | ⎭ |
Si no se separan bien los contenidos de las celdas podemos incluir la clase _bs configurable, es decir, con _bsNNN donde NNN son de 1 a 3 dígitos que, dividido entre 100, son los "em" que se aplican al estilo border-spacing que separa las celdas de la tabla. En este caso pasamos _bs50 con lo que se aplica el estilo border-spacing: 0.5em:
| ⎧ | x | x2 | x+y | ⎫ |
| ⎪ | 2x | x/y | (x+1)2 | ⎪ |
| ⎩ | x-y | 2π | √(n-1) | ⎭ |
Cabe hacer operaciones de un escalar por una matriz:
| A = 2 × | ⎧ | 2 | 15 | -7 | ⎫ |
| ⎪ | 33 | 6 | 10 | ⎪ | |
| ⎩ | 25 | 8 | 13 | ⎭ |
Y sumar matrices:
| A = 2 × | ⎧ | 2 | 15 | -7 | ⎫ | + | ⎧ | 9 | 5 | 67 | ⎫ | = |
| ⎪ | 33 | 6 | 10 | ⎪ | ⎪ | -2 | 4 | 3 | ⎪ | |||
| ⎩ | 25 | 8 | 13 | ⎭ | ⎩ | 5 | 88 | 4 | ⎭ |
O multiplicar matrices:
| A = (12, 5, 3) × | ⎧ | 2 | 15 | -7 | ⎫ |
| ⎪ | 33 | 6 | 10 | ⎪ | |
| ⎩ | 25 | 8 | 13 | ⎭ |
También podemos encerrar la matriz entre corchetes:
| A = 2 × | ⎡ | 2 | 15 | -7 | ⎤ |
| ⎢ | 33 | 6 | 10 | ⎥ | |
| ⎣ | 25 | 8 | 13 | ⎦ |
Para representar el determinante simplemente anteponemos det:
| A = det | ⎡ | 2 | 15 | -7 | ⎤ |
| ⎢ | 33 | 6 | 10 | ⎥ | |
| ⎣ | 25 | 8 | 13 | ⎦ |
O bien usamos las barras verticales ocultando la palabra det, pues al obtener la expresión se incluirá.
| A = det | ⎪ | 2 | 15 | -7 | ⎪ |
| ⎪ | 33 | 6 | 10 | ⎪ | |
| ⎪ | 25 | 8 | 13 | ⎪ |
No es usual usar llaves para representar matrices:
| ⎧ | 2 | 15 | -7 | ⎫ |
| ⎨ | 33 | 6 | 10 | ⎬ |
| ⎩ | 25 | 8 | 13 | ⎭ |
Si sólo necesitamos dos filas, podemos usar las llaves simples:
| ⎰ | 2 | 15 | -7 | ⎱ |
| ⎱ | 25 | 8 | 13 | ⎰ |
Piecewise: Definiciones de funciones para recurrencias y series
Lo siguiente podría ser la definición de una recurrencia:
| T(n) = { | 1 | si n=0 |
| T(n-1) + n | si n>0 |
El HTML escrito es el siguiente:
<table class="math _xc">
<tr><td rowspan="2">T(n) = <i class="_fs250 _vb">{</i> </td>
<td class="_al">1</td><td> si n=0</td></tr>
<tr><td>T(n-1) + n</td><td> si n>0</td></tr>
</table>La clase estructural _xc permite recuperar la expresión en lenguaje natural siguiente usando la función piecewise:
T(n) = piecewise({{1, n = 0}, {T(n - 1) + n, n>0}})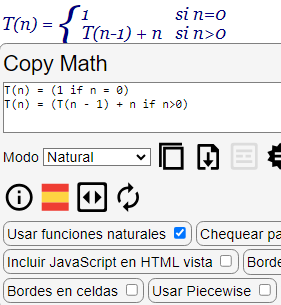
En la configuración aparece "Usar Piecewise" activado de forma predeterminada. Si lo desactivamos como se observa en la Figura usará un lenguaje más "natural":
T(n) = (1 if n = 0) T(n) = (T(n - 1) + n if n>0)
En la columna donde están los condicionales se suprime cualquier palabra y se antepone if. Esta expresión no siempre puede ser evaluada por Wolfram Alpha, pues para definir esta recurrencia hay que pasar explicítamente los valores iniciales:
{T(0) = 1, T(n) = T(n-1) + n}Si copia y pega en Wolfram Alpha la expresión anterior, verá que es capaz de resolverla.
La estructura del HTML debe ser como sigue:
- La table TABLE debe llevar
class="math _xc", donde_xces para identificar que contiene una definición de función a trozos. - Una primera fila TR con al menos 2 celdas TD seguidas sin
rowspan, que son las celdas que contienen el valor y el condicional de cada fila. El resto de los TD antes o después de este gruo de 2 deben tener unrowspanigual al número de filas que hay en la tabla. - Una o más filas siguientes con solo 2 celdas TD seguidas sin
rowspanpara el resto de parejas valor y condición. - Pueden también incluirse otras celdas antes y después de las 2 seguidas que contienen valor y condicional, pero debe llevar el atributo
class="_xn", con el estilo_xnpara paréntesis y llaves con caracteres multilínea, como veremos más abajo.
<table class="math _xc">
<tr><td rowspan="N">...{</td><td>valor</td><td>condición</td></tr>
<tr><td>valor</td><td>condición</td></tr>
<tr><td>valor</td><td>condición</td></tr>
...Total N filas
<tr><td>valor</td><td>condición</td></tr>
</table>Una función definida a trozos vendría a ser la traducción en español de "piecewise" como se observa en Wikipedia, por ejemplo:
| abs(x) = { | -x | si x<0 |
| x | si x≥0 |
La extracción en lenguaje natural nos devuelve esta expresión que puede evaluar WolframAlpha:
abs(x) = piecewise({{- x, x<0}, {x, x≥0}})Las palabras que definen las condiciones son "si" o "if", con o sin mayúsculas. Una última opción puede ponerse como "en otro caso", "de lo contrario" u "otherwise", con o sin mayúsculas. En el siguiente ejemplo usamos palabras en inglés y español con y sin mayúsculas
| f(x) = { | 1 | SI x < 1 |
| x | if 1 ≤ x ≤ 2 | |
| x2-2 | En otro caso |
La extracción en lenguaje natural sin usar Piecewise se hace con las palabras en inglés "if" y "otherwise" en minúsculas:
f(x) = (1 if x < 1) f(x) = (x if 1 ≤ x ≤ 2) f(x) = (x^2-2 otherwise)
La extracción con Piecewise nos dará lo siguiente, que WolframAlpha puede resolver.
f(x) = piecewise({{1, x < 1}, {x, 1 ≤ x ≤ 2}}, x^2-2)El HTML del ejemplo anterior es:
<table class="math _xc">
<tr><td rowspan="3">f(x) = <i class="_fs350 _fn _vb">{</i>
</td><td class="_al">1</td><td class="_al">SI x < 1</td></tr>
<tr><td class="_al">x</td><td class="_al">if 1 ≤ x ≤ 2</td></tr>
<tr><td class="_al">x<sup>2</sup>-2</td>
<td class="_al">En otro caso</td></tr>
</table>Podemos prescindir de "si" o "if" en los condicionales:
| T(n) = { | 1 | n=0 |
| T(n-1) + n | n>0 |
El HTML de lo anterior es como sigue, donde ponemos un padding-left con class="_pl100" que separa 1em de la columna previa de valores:
<table class="math _xc">
<tr><td rowspan="2">T(n) = <i class="_fs180 _fn">{</i> </td>
<td class="_al">1</td><td class="_pl100">n=0</td></tr>
<tr><td>T(n-1) + n</td><td class="_pl100">n>0</td></tr>
</table>En cualquier caso cuando lo extraemos como lenguaje natural, sin Piecewise, se agregará "if":
T(n) = (1 if n = 0) T(n) = (T(n - 1) + n if n>0)
La definición a trozos puede formar parte de una expresión en cuyo caso hay que encerrarla en paréntesis:
| g(x) = x2 + ({ | 1 | if x = 1 | ) (ex-1) |
| (x2+1) | if x ≥ 1 |
Aquí hay algunos ejemplos con definiciones de recurrencias:
| K(n, k) = { | 0 | si n<k |
| kk | si n=k | |
| n K(n-1, k) + nk | si n>k |
Como llave estamos usando el caracter "{", pero cuando incrementamos el tamaño de la fuente toma demasiado grueso. Una posibilidad es usar una fuente monoespaciada como Courier" usando la clase _ff e incluyéndola como class="_ffcourier":
| T(n) = { | 1 | si n≤2 |
| n T(n-1) + n2 + n + 1 + n n! | si n>2 |
Podría ser más elegante usar los de multilínea que vimos en un apartado anterior. Usamos símbolos UNICODE multilínea. Vea lo que expusimos en el apartado anterior sobre estos caracteres multilinea y su incorrecta visualización en algunos navegadores. Para la de dos líneas usamos los símbolos ⎰ ⎱ en una columna:
| T(n) = | ⎰ | 1 | si n≤1 |
| ⎱ | n T(n-1) + n + 1 | si n>1 |
El HTML es el siguiente, donde se observa que a las celdas que contienen los caracteres multilínea "⎰" y "⎱" se les dota del estilo _xn, que conforma estilo CSS font-style: normal; vertical-align: bottom; line-height: 0.25; display: inline-block:
<table class="math _xc">
<tr><td rowspan="2">T(n) =</td><td class="_xn _va">⎰</td><td class="_al">1</td><td class="_pl100">si n≤1</td></tr>
<tr><td class="_xn _va">⎱</td><td>n T(n-1) + n + 1</td><td class="_pl100">si n>1</td></tr>
</table>En el caso anterior sobrescribimos la alineación vertical con _va que aplica vertical-align: middle para ajustar la llave. Para más de dos líneas tenemos este ejemplo, donde prescindimos de "si" o "if":
| T(n, k) = | ⎧ | 1 | k=0 |
| 1 | n=0 | ||
| ⎨ | 2 | n=1 ∧ k=1 | |
| ⎩ | T(n-1, k-1)+1 | n>1 ∨ k>1 |
En este usamos "otherwise" como última opción:
| T(n, k) = | ⎧ | 1 | k=0 |
| 1 | n=0 | ||
| ⎨ | 2 | n=1 ∧ k=1 | |
| ⎩ | T(n-1, k-1)+1 | (otherwise) |
También podemos usarlo en una expresión
| ∑n=-∞∞ | ⎧ | ⎧ | 1 | n=0 | ⎫ | xn |
| ⎪ | ⎪ | 4 | n=1 | ⎪ | ||
| ⎪ | ⎪ | 15/2 | n=2 | ⎪ | ||
| ⎪ | ⎨ | 29/3 | n=3 | ⎪ | ||
| ⎪ | ⎪ | 21/2 | n=4 | ⎪ | ||
| ⎩ | ⎩ | 32/3 | n>4 | ⎭ |
Infinito complejo
Un infinito complejo en el plano complejo representa un valor real infinito pero con un argumento deconocido o indefinido. Para presentarlo usamos la clase _xi que combina los caracteres "∞" con "~" encima, como este ejemplo:
<div class="math">(-1)! = <i class="_xi">∞</i></div>
Al traducirlo a lenguaje natural nos devolverá (- 1)! = ComplexInfinity, pues Wolfram Alpha reconoce ComplexInfinity.