Desarreglos parciales 3
Otra forma de calcular el valor numérico de los desarreglos parciales
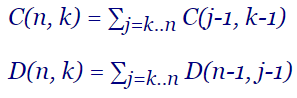
Los desarreglos parciales D(n, k) de una lista con n elementos distintos son todas las sublistas ordenadas con n elementos distintos que se pueden generar de tal forma que solo k elementos aparecen en su posición original.
En temas anteriores hemos visto que su valor numérico se puede calcular con D(n, k) = C(n, k) × D(n-k) y también con D(n, k) = n/k D(n-1, k-1). En este tema buscaremos una tercera forma con similitud con la que ya habíamos visto para las combinaciones, como se observa en la Figura.
Em el tema Combinaciones vimos una recurrencia que mejoraba el coste de la del Triángulo de Pascal C(n, k) = C(n-1, k-1) + C(n-1, k):
C(n, k) = ∑j=k..n C(j-1, k-1)
D(n, k) = ∑j=k..n D(n-1, j-1)
Implementamos ese algoritmo y otros en la herramienta Combine Tools, en la pestaña "Numéricos", donde ejecutamos algoritmos para obtener el valor numérico de funciones combinatorias como esa:
// C(n, k) = sum_(j=k)^n C(j-1, k-1)
function binomial2(n, k) {
if (k===0) {
return 1;
} else {
let value = 0;
for (let j=k; j<=n; j++){
value += binomial2(j-1, k-1);
}
return value;
}
}Dado que para los desarreglos parciales tenemos la fórmula D(n, k) = C(n, k) × !(n-k) que está relacionada con las combinaciones, he probado algo muy similar a [1] para obtener los desarreglos parciales:
0 ≤ m ≤ b
D(b, m) = !b
D(n, k) = ∑j=k..n D(n-1, j-1)
El argumento b = n0 - k0 toma los valores iniciales de n, k permaneciendo esa diferencia constante en el transcurso de ejecución de la recurrencia. Es, por tanto, un valor que interviene en la recurrencia solo para determinar el caso base n=b. Como veremos en el siguiente apartado, es vital entender su comportamiento. Por otro lado m no interviene en la recurrencia, pues los casos bases se producen cuando n=b independientemente del valor de m.
// D(n, k) = sum_(j=k)^(n) D(n-1, j-1)
function partialDerange4(n, k, b=n-k) {
if (n===b) {
return subfactorial(b);
} else {
let value = 0;
for (let j=k; j<=n; j++){
value += partialDerange4(n-1, j-1);
}
return value;
}
}Este algoritmo partialDerange4(n, k) funciona produciendo los mismos valores que con las otras alternativas que implementamos en la herramienta usando principios matemáticos que ya hemos visto en temas anteriores:
partialDerange1(n, k)usando D(n, k) = C(n, k) × !(n-k)partialDerange2(n, k)usando D(n, 0) = !n, D(n, k) = n/k D(n-1, k-1)partialDerange3(n, k)usando D(n, 0) = !n, D(n, k) = !(n-k) ∑j=k..n C(j-1, k-1)
Vea que partialDerange3(n, k) es igual que partialDerange1(n, k) sólo que cambiando C(n, k) por ∑j=k..n C(j-1, k-1) tal como vimos en [1].
El que estamos viendo en este tema partialDerange4(n, k) produce los mismos valores que esos tres, pero no me es fácil demostrar esa base matemática en la que se sustenta. En el siguiente apartado intentaremos indagar más sobre esto.
En el siguiente desarrollo esquemático de partialDerange4(5, 3) vemos como obtenemos el valor correcto D(5, 3) = 10, observando como evoluciona la ejecución del algoritmo:
b = 5 -3 = 2
D(5, 3) = sum_(j=3..5) D(4, j-1)
D(4, 2) = sum_(j=2..4) D(3, j-1)
D(3, 1) = sum_(j=1..3) D(2, j-1)
D(2, 0) = !2
D(2, 1) = !2
D(2, 2) = !2
D(3, 2) = sum_(j=2..3) D(2, j-1)
D(2, 1) = !2
D(2, 2) = !2
D(3, 3) = sum_(j=3..3) D(2, j-1)
D(2, 2) = !2
D(4, 3) = sum_(j=3..4) D(3, j-1)
D(3, 2) = sum_(j=2..3) D(2, j-1)
D(2, 1) = !2
D(2, 2) = !2
D(3, 3) = sum_(j=3..3) D(2, j-1)
D(2, 2) = !2
D(4, 4) = sum_(j=4..4) D(3, j-1)
D(3, 3) = sum_(j=3..3) D(2, j-1)
D(2, 2) = !2Vemos que se producen diez casos bases resaltados en amarillo y por tanto el resultado es el esperado D(5, 3) = 10 × !2 = 10 pues !2 = 1.
El Triágulo de Pascal en desarreglos parciales
Intentando entender el comportamiento de D(n, k) = ∑j=k..n D(n-1, j-1) veamos antes el comportamiento de C(n, k) = ∑j=k..n C(j-1, k-1), por ejemplo para C(7, 2) tenemos:
Esto se observa en la siguiente tabla de valores
| n↓k→ | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 2 | 1 | 0 | 0 |
| 3 | 1 | 3 | 3 | 1 | 0 |
| 4 | 1 | 4 | 6 | 4 | 1 |
| 5 | 1 | 5 | 10 | 10 | 5 |
| 6 | 1 | 6 | 15 | 20 | 15 |
| 7 | 1 | 7 | 21 | 35 | 35 |
| 8 | 1 | 8 | 28 | 56 | 70 |
Si desplegamos esa recurrencia de combinaciones C(n, k) = ∑j=k..n C(j-1, k-1) llegamos a esto, tal como vimos en el tema combinaciones
Se obtiene C(n+1, k+1) = C(n, k) + C(n, k+1), que actuando sobre índices nos conduce a la conocida fórmula del Triángulo de Pascal C(n, k) = C(n-1, k-1) + C(n-1, k) que se cumple para las combinaciones, como se observa en la tabla siguiente por ejemplo con los valores resaltados C(7, 2) = C(6, 1) + C(6, 2) donde 21 = 6 + 15
| n↓k→ | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 2 | 1 | 0 | 0 |
| 3 | 1 | 3 | 3 | 1 | 0 |
| 4 | 1 | 4 | 6 | 4 | 1 |
| 5 | 1 | 5 | 10 | 10 | 5 |
| 6 | 1 | 6 | 15 | 20 | 15 |
| 7 | 1 | 7 | 21 | 35 | 35 |
| 8 | 1 | 8 | 28 | 56 | 70 |
Haciendo lo mismo para los desarreglos D(n, k) = ∑j=k..n D(n-1, j-1) Para el ejemplo D(7, 2) tenemos
obteniéndose un valor que no coincide con el esperado, como se observa en la tabla de valores
| n↓k→ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 2 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4 | 9 | 8 | 6 | 0 | 1 | 0 | 0 | 0 | 0 |
| 5 | 44 | 45 | 20 | 10 | 0 | 1 | 0 | 0 | 0 |
| 6 | 265 | 264 | 135 | 40 | 15 | 0 | 1 | 0 | 0 |
| 7 | 1854 | 1855 | 924 | 315 | 70 | 21 | 0 | 1 | 0 |
| 8 | 14833 | 14832 | 7420 | 2464 | 630 | 112 | 28 | 0 | 1 |
Por otro lado desplegando la recurrencia
Donde obtenemos D(n+1, k+1) = - D(n, k-1) + D(n+1, k), que ajustando índices obtendríamos D(n, k) = - D(n-1, k-2) + D(n, k-1). Esto no se parece en nada a la de las combinaciones y ni siquiera funciona, pues debería cumplirse D(7, 2) = - D(6, 0) + D(7, 1) y vemos que no se cumple 924 ≠ -265 + 1855 = 1590
Si aplicamos algo parecido al Triángulo de Pascal con D(n, k) = D(n-1, k-1) + D(n-1, k) también parece no funcionar, pues para D(7, 2) = D(6, 1) + D(6, 2) con lo que tenemos 924 ≠ 264 + 135, como se observa en la tabla de valores:
| n↓k→ | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 1 | 0 | 0 |
| 3 | 2 | 3 | 0 | 1 | 0 |
| 4 | 9 | 8 | 6 | 0 | 1 |
| 5 | 44 | 45 | 20 | 10 | 0 |
| 6 | 265 | 264 | 135 | 40 | 15 |
| 7 | 1854 | 1855 | 924 | 315 | 70 |
| 8 | 14833 | 14832 | 7420 | 2464 | 630 |
En la expresión D(n, k) estamos obviando el argumento b = n0 - k0 que es el que se obtiene con los valores iniciales. Por lo tanto es mejor expresarlo con ese tercer argumento, que interviene en la recurrencia más bien como un parámetro constante que como una variable como ya habíamos dicho:
Vease que para D(n, k) y para D(n-1, k-1) se cumple que b = n0-k0 = n-k = n-1-(k-1), pues cuando ambas variables n, k se incrementan o decremetan en la misma cantidad, la diferencia n - k permanece constante y es igual que la inicial b.
Sin embargo en lo resaltado en amarillo de la expresión anterior vemos que la diferencia ha cambiado n-1-k = b-1, con lo que D(n-1, k) ≠ D(n-1, k, b-1). Para el ejemplo que vemos en la tabla tenemos D(6, 2, 4) = 135 con n-k=4. Y necesitamos el valor con b=5 para producir D(6, 2, 5) = 660, pues 924 = 264 + 660. Para ello aplicamos la siguiente fórmula:
| D(n, k) = D(n-1, k-1) + | !b | × D(n-1, k, b-1) |
| !(b-1) |
con lo que obtenemos el comportamiento correcto:
| 924 = 264 + | !5 | × 135 | = 264 + | 44 | × 135 = 264 + 660 |
| !4 | 9 |
Usando la herramienta Combine Tools podemos obtener la siguiente tabla de valores (pestaña "Numéricos", botón "Listar PD"), observando la pareja de valores para n=7, k=2 con 924, 924, donde el primer valor se obtiene aplicando el algoritmo partialDerange4(n, k) y la segunda usando la identidad [4] anterior. Coincide en todos los casos menos en aquellos donde !(b-1) = 0 y por tanto se produce una indeterminación que impide obtener ese valor (lo representamos con "?").
| n↓k→ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1,? | |||||||
| 2 | 0,0 | 1,? | ||||||
| 3 | 3,? | 0,0 | 1,? | |||||
| 4 | 8,8 | 6,? | 0,0 | 1,? | ||||
| 5 | 45,45 | 20,20 | 10,? | 0,0 | 1,? | |||
| 6 | 264,264 | 135,135 | 40,40 | 15,? | 0,0 | 1,? | ||
| 7 | 1855,1855 | 924,924 | 315,315 | 70,70 | 21,? | 0,0 | 1,? | |
| 8 | 14832,14832 | 7420,7420 | 2464,2464 | 630,630 | 112,112 | 28,? | 0,0 | 1,? |
Si la expresión [4] es cierta entonces [3] refleja la aplicación del algoritmo partialDerange4(n, k) que usa un sumatorio de forma similar al de las combinaciones binomial2(list, k). Lo que implica que la recurrencia D(n, k) = D(n-1, k-1) + D(n-1, k) obedece a la aplicación del algoritmo partialDerange4(n, k). Y esto es vital para demostrar su veracidad aplicando la técnica de la función generadora como veremos a continuación.
Función generadora para la recurrencia de desarreglos parciales
Vamos a demostrar que el siguiente algoritmo produce los desarreglos parciales cuya fórmula cerrada es D(n, k) = !b C(n, k) siendo b=n-k usando la técnica de la función generadora:
// D(n, k) = sum_(j=k)^(n) D(n-1, j-1)
function partialDerange4(n, k, b=n-k) {
if (n===b) {
return subfactorial(n);
} else {
let value = 0;
for (let j=k; j<=n; j++){
value += partialDerange4(n-1, j-1);
}
return value;
}
}Recordamos la base matemática de la recurrencia
0 ≤ m ≤ b
D(b, m) = !b
D(n, k) = ∑j=k..n D(n-1, j-1)
cuyo resultado, como vimos en el apartado anterior, produce la siguiente recurrencia que suponemos cierta:
Incrementando índices
Aplicaremos la función generadora
Condiciones iniciales
Observe que para cualquier n el caso base se produce cuando n = b = n0 - k0 y eso sucederá cuando k=0. Por eso D(n, 0) = D(b, 0) = !b.
| Gn,0(x, y) = ∑n≥0 D(n, 0) xn = | !b |
| 1-x |
Aplicando la función generadora a [5]:
Expresemos D(n+1, k+1) en función de D(n, k)
| = | !b | + 1 - 1 + ∑n,k≥0 D(n+1, k+1) xn+1 yk+1 = |
| 1-x |
| = | !b | + xy ∑n,k≥0 D(n+1, k+1) xn yk |
| 1-x |
De donde
| ∑n,k≥0 D(n+1, k+1) xn yk = | 1 | ( G(x, y) - | !b | ) |
| xy | 1-x |
Expresemos D(n, k+1) en función de D(n, k)
| = | !b | + ∑n,k≥0 D(n, k+1) xn yk+1 = |
| 1-x |
| = | !b | + y ∑n,k≥0 D(n, k+1) xn yk |
| 1-x |
De donde
| ∑n,k≥0 D(n, k+1) xn yk = | 1 | ( G(x, y) - | !b | ) |
| y | 1-x |
Aplicando a [6]
| 1 | ( G(x, y) - | !b | ) = G(x, y) + | 1 | ( G(x, y) - | !b | ) |
| xy | 1-x | y | 1-x |
De donde obtenemos la función generadora:
| G(x, y) = | !b |
| 1-x-xy |
Multiplicamos y dividimos por 1-y
| G(x, y) = | !b (1-y) | = |
| (1-y)(1-x-xy) |
| = | !b | - | !b y | = |
| (1-y)(1-x-xy) | (1-y)(1-x-xy) |
El término general es entonces
Como j≤k ajustamos índices teniendo en cuenta que
con lo que obtenemos
Vemos que obtenemos el resultado esperado D(n, k) = !b C(n, k), por lo que debe ser cierta la suposición D(n, k) = D(n-1, k-1) + D(n-1, k) que nos da una expresión similar al Triángulo de Pascal para los desarreglos parciales.
Usando despliegue de la recurrencia
Si aún tenemos dudas con el apartado anterior, intentemos aplicar la técnica del despliegue de la recurrencia, que era la siguiente, donde m no interviene como explicamos en el primer apartado:
0 ≤ m ≤ b
D(b, m) = !b
D(n, k) = ∑j=k..n D(n-1, j-1)
Para desplegarla hacemos b=n-k, k=n-b quedando
Como la longitud j=n-b..n del sumatorio es n-(n-b)+1 = b+1, se puede hacer corresponder con un rango j=0..b, con lo que podemos usar esta recurrencia equivalente:
D(n, n-b) = ∑j=0..b D(n-1, n-b+j-1)
Como la resta de los argumentos de D(n, n-b) es n-(n-b) = b podemos expresar lo anterior usando p=n-b, con la condición de que la llamada inicial sea D(n, n-b)
D(n, p) = ∑j=0..(n-p) D(n-1, p+j-1)
Inicio: D(n, n-b)
Esta recurrencia debe tener la solución !(n-k) C(n, k) que es la de los desarreglos parciales. Para verlo desplegamos usando el ejemplo con b=2. Identificamos las llamadas recursivas, siendo la primera i=0.
Aplicando D(n, p) = ∑j=0..(n-p) D(n-1, p+j-1) a cada término
Volviendo a [7]
Volviendo a aplicar D(n, p) = ∑j=0..(n-p) D(n-1, p+j-1) a cada término
Sustituyendo en [8]
Observamose en [7], [8] y [9] las secuencias de coeficientes resaltados, donde i representa cada llamada recursiva:
i=1 ⇒ 1, 2, 3
i=2 ⇒ 1, 3, 6
Estos valores se corresponden con las diagonales de los binomiales C(i, i), C(i+1, i), C(i+2, i)
| n↓k→ | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
| 2 | 1 | 2 | 1 |
| 3 | 1 | 3 | 3 |
| 4 | 1 | 4 | 6 |
i=1 ⇒ 1, 2, 3 = C(1, 1) + C(2, 1) + C(3, 2)
i=2 ⇒ 1, 3, 6 = C(2, 2) + C(3, 2) + C(4, 2)
Podemos expresar [9] en una llamada i-ésima genérica:
C(i, i) D(n-i-1, n-i-3) + C(i+1, i) D(n-i-1, n-i-2) + C(i+2, i) D(n-i-1, n-i-1)
Cuando lleguemos a la llamada recursiva i=n-(b+1) = n-3 estaremos en el final:
C(n-3+1, n-3) D(n-(n-3)-1, n-(n-3)-2) +
C(n-3+2, n-3) D(n-(n-3)-1, n-(n-3)-1)
llegando a los casos bases D(2, 0), D(2, 1), D(2, 2)
Como D(2, 0) = D(2, 1) = D(2, 2) = !2 entonces
Observando que C(n, 2) = C(n, n-2) y, en general C(n, k) = C(n, n-k) = n!/(k!(n-k)!), pudiendo comprobarse en WolframAlpha, por lo que demostramos para b=2 que hemos llegado a la fórmula D(n, n-b) = !b C(n, b) o bien D(n, k) = !(n-k) C(n, k). En cuanto a la suma de binomiales:
cumple la expresión que vimos en [1] sobre las combinaciones, que era otra forma de obtenerlas C(n, k) = ∑j=k..n C(j-1, k-1) siendo k=n-2.
Generalizando para cualquier valor de b
C(n-b-1, n-b-1) D(b, 0) + C(n-b, n-b-1) D(b, 1) + ... + C(n-1, n-b-1) D(b, b) =
Que siendo k=n-b resulta D(n, k) = !(n-k) C(n, k) con lo que parece ser cierta la validez de la recurrencia dada D(n, k) = ∑j=k..n D(n-1, j-1) para calcular el valor numérico de los desarreglos parciales.
Esta forma de desplegar la recurrencia con un sumatorio la usaremos en el tema siguiente para buscar el término general de un algoritmo para generar desarreglos parciales.