Desarreglos parciales 4
Desarreglos parciales: Implementando la tercera recurrencia
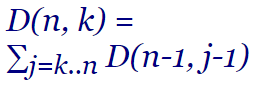
Los desarreglos parciales D(n, k) de una lista con n elementos distintos son todas las sublistas ordenadas con n elementos distintos que se pueden generar de tal forma que solo k elementos aparecen en su posición original.
En un tema anterior vimos otra fórmula recurrente D(n, k) = n/k D(n-1, k-1) para obtener el valor numérico de los desarreglos parciales. Debido al cociente n/k, vimos allí las dificultades para usarla como base de implementación de un algoritmo para generar los desarreglos. Por eso en el siguiente tema buscábamos una nueva recurrencia que nos permitiera obtener el valor númerico de los desarreglos parciales:
0 ≤ m ≤ b
D(b, m) = !b
D(n, k) = ∑j=k..n D(n-1, j-1)
Recordemos que el valor b = n0 - k0 se mantiene constante en la ejecución, pues proviene de la diferencia que inicialmente tienen las variables n, k. Vamos a usar esa base para implementar un algoritmo que genere los desarreglos parciales.
Algoritmo derangeP3(list, k) para generar desarreglos parciales
Usando como base esa recurrencia, implementamos el siguiente algoritmo para generar los desarreglos parciales:
// D(n, k) = sum_(j=k..n) D(n-1, j-1)
function derangeP3(list=[], k=0, p=-k, b=list.length-k)
let result = [];
let n = list.length;
if (n===b) {
/* iter += Td(n-k) */
result = derange1(list);
} else {
iter += 1;
for (let j=k; j<=n; j++){
iter += 1;
let jk = j+p;
let pivot = list[jk];
iter += n-1;
let listMinor = [ ...list.slice(0, jk), ...list.slice(jk+1)];
let subResult = derangeP3(listMinor, j-1, p+1, b);
/* subResult.length = !b * C(2n-j-b-1, n-b-1) */
for (let i=0; i<subResult.length; i++) {
/* subResult[i].length = n-1 */
iter += 1 + subResult[i].length;
result.push([...subResult[i].slice(0, jk), pivot,
...subResult[i].slice(jk)]);
}
}
}
return result;
}Con b = n0 - k0 constante durante toda la ejecución, pues se inicia con los valores iniciales n0 y k0, pasamos esa variable b como argumento en cada llamada con objeto de tenerlo disponible para el caso base n=b, en cuyo caso devolvemosTd(b) que son los desarreglos sin puntos fijos que obtuvimos con el primer algoritmo implementado derange1(list).
Usamos otro argumento p que iniciamos con p=-k que no intervendrá en la recurrencia, pues sólo sirve a efectos de seleccionar el pivote adecuado en el algoritmo. Como hacíamos con los algoritmos de recorte, recortamos la lista y llamamos nuevamente decrementanto el argumento j. E incrementando el argumento p para seleccionar otro pivote en la siguiente llamada.
No siempre es fácil ver esquemáticamente como evoluciona el algoritmo. Intentemos explicarlo usando el ejemplo D(abcd, 2) = {abdc, adcb, acbd, dbca, cbad, bacd}
D(abcd, 2)
j=2 p=a -> D(bcd, 1)
j=2 p=b -> D(cd, 1) => dc +=> bdc +=> abdc
j=3 p=c -> D(bd, 2) => db +=> dcb +=> adcb
j=4 p=d -> D(bc, 3) => cb +=> cbd +=> acbd
j=3 p=b -> D(acd, 2)
j=3 p=c -> D(ad, 2) => da +=> dca +=> dbca
j=4 p=d -> D(ac, 3) => ca +=> cad +=> cbad
j=4 p=c -> D(abd, 3)
j=4 p=d -> D(ab, 3) => ba +=> bad +=> bacd
Result = abdc, adcb, acbd, dbca, cbad, bacdIteramos por el bucle j=k..n que en el ejemplo será j=2..4. El pivote se elige adecuadamente en cada iteración, desde el inicio de cada lista al inicio de cada bucle, pero luego se desplaza. Cuando llegamos a una lista con dos elementos estamos en el caso base y devolvemos => la lista invertida. Con +=> representamos la recomposición del resultado en las devoluciones de llamadas, que se produce en el bucle final que maneja subResult. Cada pivote se inserta en su sitio con respecto a la lista desde donde fue extraido. Al final obtenemos el resultado esperado, pues en cada desarreglo hay exactamente 2 pivotes en su sitio, es decir, 2 elementos están en su posición inicial mientras que el resto no lo están (están desarreglados).
Observando el algoritmo planteamos la recurrencia siguiente
Si recordamos que los desarreglos parciales son D(n, k) = !b C(n, k), vemos que el tamaño de subResult es !b C(n-j+k-1, k-1) con fórmula similar a la dada. Observe que en el código pusimos el comentario
pues sabiendo que b=n-k es constante en la ejecución, tenemos que ese binomial que vemos en el comentario queda así, tal como pusimos antes en [1]:
Veáse que subResult es el resultado de la llamada let subResult = derangeP3(listMinor, j-1, p+1, b), con los argumentos D(n, k) = D(n-1, j-1), es decir, j-1 ≡ k-1, por lo que nos queda !b C(n-j+k-1, k-1) ∧ j=k ⇒ !b C(n-k+k-1, k-1) = !b C(n-1, k-1), que es el valor numérico de los desarreglos con la llamada D(n-1, k-1), manteniéndose b = n-1-(k-1) = n-k constante con la llamada inicial.
Simplificamos un poco [1]
Esta recurrencia con dos variables n, k no es fácil de resolver. Para intentar algo podemos resolver lo siguiente, viendo que b = n - k ⇒ k = n - b y además tal como vimos en el comentario del código antes:
Con esto la recurrencia queda así, dependiente sólo de n pues b es constante:
Despliegue con b=0
Usaremos la técnica del despliegue para ver si conseguimos una fórmula general. Empezamos con b=0, sabiendo que !0 = 1. Empezamos con la llamada inicial, identificando cada llamada recursiva con la variable i:
Observe que no desplegamos el primer sumatorio, sólo el segundo que contiene la nueva llamada recursiva.
1 + ∑j=n-2..n-2 ( (n-2) + !0 (n-2) C(2(n-1)-j-1, (n-1)-1) ) + T(n-3, n-3)
Ya vemos cierta consistencia por lo que vamos a suponer el caso cuando i=n-1
1 + ∑j=n-(n-1)..n-(n-1) ((n-(n-1))+!0 (n-(n-1)) C(2(n-(n-1))-j-1, (n-(n-1))-1)) +
T(n-n, n-n)
Al llegar a la llamada n-1 encontramos el caso base T(n-n, n-n) = T(0, 0) = Td(0) = 3 cuyo valor es el del algoritmo derange1(list). Sumando las llamadas i podemos expresarlo así:
Si resolvemos con WolframAlpha obtendremos:
Expandiendo en valores desde n=0 obtenemos T(n, n) = 3, 6, 11, 18, 27, 38, 51, 66, ... tal como se observa en la siguiente tabla, que se obtiene en la aplicación Combine Tools, donde resaltamos en amarillo la secuencia correspondiente a T(n, n) con b=n-k=0:
| n↓k→ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 4 | 6 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 11 | 13 | 11 | 1 | 1 | 1 | 1 | 1 |
| 3 | 39 | 52 | 27 | 18 | 1 | 1 | 1 | 1 |
| 4 | 173 | 205 | 142 | 47 | 27 | 1 | 1 | 1 |
| 5 | 943 | 1116 | 635 | 309 | 74 | 38 | 1 | 1 |
| 6 | 6115 | 7279 | 4191 | 1549 | 588 | 109 | 51 | 1 |
| 7 | 45993 | 55840 | 31990 | 12046 | 3268 | 1021 | 153 | 66 |
| 8 | 393433 | 486665 | 282780 | 105111 | 29251 | 6235 | 1657 | 207 |
| 9 | 3770283 | 4742452 | 2790765 | 1048811 | 286592 | 63074 | 11036 | 2552 |
| 10 | 39996671 | 51052531 | 30387205 | 11527529 | 3178834 | 684457 | 124393 | 18421 |
En verde tenemos la secuencia para T(n, n-1) con b=n-k=1 y en azul para T(n, n-2) con b=n-k=2 que desarrollaremos a continuación.
Despliegue con b=1
Recordemos la recurrencia
que particularizamos para b=1
Empezamos con la llamada inicial:
∑j=n-1..n-1 T(n-2, j-1) =
Y la otra llamada
∑j=n-2..n-1 T(n-2, j-1) =
T(n-2, n-3) + T(n-2, n-2)
Sumando ambas
1 + ∑j=n-1..n-1 ( (n-1) + !1 (n-1) C(2(n-1)-j-2, (n-1)-2) ) +
1 + ∑j=n-2..n-1 ( (n-1) + !1 (n-1) C(2(n-1)-j-2, (n-1)-2) ) +
2 T(n-2, n-2) + T(n-2, n-3)
Prescidiendo del desarrollo para abreviar obtenemos:
2 + 2 ∑j=n-2..n-2 ( (n-2) + !1 (n-2) C(2(n-2)-j-2, (n-2)-2) ) +
1 + 1 ∑j=n-3..n-2 ( (n-2) + !1 (n-2) C(2(n-2)-j-2, (n-2)-2) ) +
3 T(n-3, n-3) + T(n-3, n-4)
Prescidiendo del desarrollo para abreviar obtenemos:
3 + 3 ∑j=n-3..n-3 ( (n-3) + !1 (n-3) C(2(n-3)-j-2, (n-3)-2) ) +
1 + 1 ∑j=n-4..n-3 ( (n-3) + !1 (n-3) C(2(n-3)-j-2, (n-3)-2) ) +
4 T(n-4, n-4) + T(n-4, n-5)
Ya podemos llegar a una solución con el caso base en la llamada i=n-2, y aunque no lo vamos a presentar para abreviar, pues solo tenemos que sumar todo lo resaltado desde i=0 hasta i=n-2
Por un lado tenemos el caso base en b=1 con T(1, 1) = T(1, 0) = Td(1) = 4, con lo que (n-1) T(1, 1) + T(1, 0) = 4 n. Por otro lado en lo anterior vemos dos grupos de sumas observando los índices de los sumatorios, un primer grupo con los que tienen índices como n-1..n, n-2..n-1, n-3..n-2, ...
Y un segundo grupo con los que tienes índices como n-1..n-1, n-2..n-2, n-3..n-3, ...
Por lo tanto podemos aplicar una suma a la llamadas
Vea que podemos ampliar el segundo sumatorio a i=0 pues en ese caso el primer término será cero:
∑i=0..n-2 ( 1 + ∑j=n-i-1..n-i ( (n-i) + !1 (n-i) C(2(n-i)-j-2, (n-i)-2) )) +
∑i=0..n-2 ( i + i ∑j=n-i..n-i ( (n-i) + !1 (n-i) C(2(n-i)-j-2, (n-i)-2) )) +
4n
Para resolver esto y obtener algo más practicable observamos que !1 = 0
Resolvamos los sumatorios interiores ∑j=n-i-1..n-i (n-i) = 2(n-i) y el otro sumatorio quedará como ∑j=n-i..n-i (n-i) = n-i con lo que tenemos finalmente:
Podemos resolverlo con WolframAlpha obteniendo:
Expandiendo esta fórmula obtenemos la secuencia para n≥1 ⇒ T(n, n-1) = 4, 13, 27, 47, 74, 109, 153, 207, ... (ver en WA), la misma que vemos en la tabla de valores resaltados en verde más arriba.
Despliegue con b=2
Recordemos la recurrencia
que particularizamos para b=2
Aunque he realizado el despliegue completo hasta b=4 (ver documento de trabajo en derangep3.txt), no voy a exponer todo eso pues es muy largo. Para abreviar, tenemos con b=1 el desglose de sumas que vimos en [1] y lo aplicamos a b=2:
Llegando hasta b=4 se observa que los términos antes del sumatorio interno son de la forma
que equivale a
Por otro lado el término 1/2 n(n-1) × 39 para los tres casos vistos b=0 a b=2 así como para b=3 y b=4 que he desplegado también:
Se identifica el término general con este sumatorio:
pues, por ejemplo para b=2 tenemos ∑j=0..2 C(n+j-3, j) = 1/2 n(n-1). Con esto el despliegue para b=2 queda así con un forma más generalizada:
∑i=0..n-3 C(i-1, 0) ( 1 + ∑j=n-i-2..n-i ( (n-i) + !2 (n-i) C(2(n-i)-j-3, (n-i)-3) )) +
∑i=0..n-3 C(i, 1) ( 1 + ∑j=n-i-1..n-i ( (n-i) + !2 (n-i) C(2(n-i)-j-3, (n-i)-3) )) +
∑i=0..n-3 C(i+1, 2) ( 1 + ∑j=n-i..n-i ( (n-i) + !2 (n-i) C(2(n-i)-j-3, (n-i)-3) )) +
∑j=0..2 C(n+j-3, j) × 11
Resolvemos primero los sumatorios interiores
Y luego los exteriores:
1/24 (n-2)(3n3+8n2+49n+156) +
1/12 (n-3)(n-2)(n2+7n+34) +
1/12 (n-3)(n-2)(n-1)(n+10) +
11/2 (n-1)n
con lo que llegamos al término final:
Al expandirlo obtenemos la secuencia para n≥2 ⇒ T(n, n-2) = 11, 52, 142, 309, 588, 1021, 1657, 2552, ... tal como obtuvimos en la tabla de valores resaltados en azul.
Deduciendo el término general
Repitiendo aquí las soluciones que hemos visto para b=0
∑i=0..n-1 C(i-1, 0) ( 1 + ∑j=n-i..n-i ( (n-i) +!0 (n-i) C(2(n-i)-j-1, (n-i)-1)) +
∑j=0..0 C(n+j-1, j) × Td(0)
para b=1
∑i=0..n-2 C(i-1, 0) ( 1 + ∑j=n-i-1..n-i ( (n-i) + !1 (n-i) C(2(n-i)-j-2, (n-i)-2) )) +
∑i=0..n-2 C(i, 1) ( 1 + ∑j=n-i..n-i ( (n-i) + !1 (n-i) C(2(n-i)-j-2, (n-i)-2) )) +
∑j=0..1 C(n+j-2, j) × Td(1)
y para b=2
∑i=0..n-3 C(i-1, 0) ( 1 + ∑j=n-i-2..n-i ( (n-i) + !2 (n-i) C(2(n-i)-j-3, (n-i)-3) )) +
∑i=0..n-3 C(i, 1) ( 1 + ∑j=n-i-1..n-i ( (n-i) + !2 (n-i) C(2(n-i)-j-3, (n-i)-3) )) +
∑i=0..n-3 C(i+1, 2) ( 1 + ∑j=n-i..n-i ( (n-i) + !2 (n-i) C(2(n-i)-j-3, (n-i)-3) )) +
∑j=0..2 C(n+j-3, j) × Td(2
podemos entonces suponer que para un término génerico b tenemos este despliegue:
∑i=0..n-(b+1) C(i-1, 0) ( 1 + ∑j=n-i-(b-0)..n-i ( (n-i) + !b (n-i) C(2(n-i)-j-(b+1), (n-i)-(b+1)) )) +
∑i=0..n-(b+1) C(i, 1) ( 1 + ∑j=n-i-(b-1)..n-i ( (n-i) + !b (n-i) C(2(n-i)-j-(b+1), (n-i)-(b+1)) )) +
∑i=0..n-(b+1) C(i+1, 2) ( 1 + ∑j=n-i-(b-2)..n-i ( (n-i) + !b (n-i) C(2(n-i)-j-(b+1), (n-i)-(b+1)) )) +
···
∑i=0..n-(b+1) C(i+b-1, b) ( 1 + ∑j=n-i..n-i ( (n-i) + !b (n-i) C(2(n-i)-j-(b+1), (n-i)-(b+1)) )) +
∑j=0..b C(n+j-(b+1), j) × Td(b)
Sumando
( 1 +∑j=n-i-(b-h)..n-i ( (n-i) + !b (n-i) C(2(n-i)-j-(b+1), (n-i)-(b+1)) )))+
∑j=0..b C(n+j-(b+1), j) × Td(b)
Ahora deshacemos el cambio b = n - k
( 1 + ∑j=k-i+h..n-i ((n-i) + !(n-k) (n-i) C(n+k-j-2i-1, k-i-1)) )) +
∑j=0..n-k C(j+k-1, k-i-1) Td(n-k)
Finalmente hacemos un ajuste con Max() para los casos cuando n<k, en cuyo caso el coste es uno, llegando a la fórmula final que coincide con el contaje de iteraciones en el algoritmo para generar los desarreglos parciales:
( 1 + ∑j=k-i+h..n-i ((n-i) + !(n-k) (n-i) C(n+k-j-2i-1, k-i-1)) )) +
∑j=0..n-k C(j+k-1, k-i-1) Td(n-k))
Implementamos el cálculo de esta extensa fórmula con este código en la herramienta:
valueCost: function(n, k) {
let b = n-k;
let sf = subfactorial(b);
let value = 0;
for (let h=0; h<=b; h++) {
for (let i=0; i<=k-1; i++) {
let val = 1;
for (let j=k-i+h; j<=n-i; j++) {
val += (n-i) + sf * (n-i) * binomial(n+k-j-2*i-1, k-i-1);
}
value += binomial(i+h-1, h) * val;
}
}
let val = 0;
for (let j=0; j<=b; j++) {
val += binomial1(j+k-1, j);
}
value += val * codesFunc.derange1.valueCost(b)[0];
return [Math.max(1, value)];
}Dada la complejidad del despliegue, creo que no será fácil aplicar la técnica de la función generadora, por lo que nos quedaremos con lo obtenido.
Comparando costes de algoritmos para generar desarreglos parciales
Comparamos los tres algoritmos implementados para generar desarreglos parciales
- derangeP1(list, k) usando D(n, k) = C(n, k) × D(n-k) donde D(n-k) se resuelve con los desarreglos usando derange1(list)
- derangeP2(list, k) usando D(n, k) = n/k D(n-1, k-1)
- derangeP3(list, k) de este tema usando D(n, k) = ∑j=k..n D(n-1, j-1)
En la siguiente tabla comparamos costes para k=3:
| n | T(n, 3) | ||
|---|---|---|---|
| derangeP1(n, 3) | derangeP2(n, 3) | derangeP3(n, 3) | |
| 0 | 6 | 1 | 1 |
| 1 | 7 | 1 | 1 |
| 2 | 8 | 1 | 1 |
| 3 | 31 | 99 | 18 |
| 4 | 29 | 214 | 47 |
| 5 | 299 | 1762 | 309 |
| 6 | 1240 | 9264 | 1549 |
| 7 | 10385 | 73957 | 12046 |
| 8 | 89872 | 647098 | 105111 |
| 9 | 897035 | 6447488 | 1048811 |
| 10 | 9837314 | 21313858 | 11527529 |
Para n≥3 el que tiene menor coste es derangeP1, pues no es un recursivo directo, usando combine2() y derange1() en un bucle que componía los resultados. En cambio derangeP2 y derangeP3 si son recursivos directos, usando un algoritmo de recorte de listas. derangeP2 es más costoso debido a que había que remover duplicados.