Variaciones con repetición
Variaciones con repetición
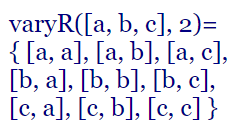
Las variaciones con repetición de una lista con n elementos distintos son todas las sublistas ordenadas con k elementos no necesariamente distintos que se pueden extraer. Su valor es VR(n, k) = nk
Ya hemos dicho en temas anteriores que las variaciones es un concepto que matemáticamente se considera como un caso particular de las permutaciones P(n, k) = n!/(n-k)!, denominadas como permutación parcial o k-permutación. Y que las variaciones con repetición se suelen considerar como permutaciones con repetición, tal como se observa en ese enlace de Wikipedia. Pero en estos temas consideramos que las permutaciones con repetición son otra cosa (que vimos en ese tema anterior) y que otros denominan como multinomial o coeficientes multinomiales.
Las variaciones con repetición de la lista [a, b, c] son las sublistas siguientes:
Observe que representamos las sublistas como Arrays, pues el orden si importa en este caso. Por ejemplo, un resultado es [a, b] que es distinto de [b, a]. El número de sublistas es VR(3, 2) = 32 = 9.
Algoritmo para generar las variaciones con repetición (varyR1)
El algoritmo para generar las variaciones con repetición es el siguiente:
// VR(n, k) = n^k = n × n^(k-1) = n × VR(n, k-1)
function varyR1(list=[], k=0, res=Array.from({length:k}, ()=>""),
result=[], n0=list.length, k0=res.length){
if (k===0){
//iter += 1;
//if (withCopyCost) iter += res.length;
result.push(copy(res));
} else {
//iter += 1;
for (let j=0; j<n0; j++){
//iter += 1;
res[k0-k] = list[j];
varyR1(list, k-1, res, result);
}
}
return result;
}La definición de la recurrencia se deduce de ese algoritmo, siendo el caso base cuando k=0. En otro caso hay una iteración más un bucle de longitud n llamadas a un tamaño inferior, más otra iteración interior en el bucle 1 + n (T(n, k-1) + 1) quedando así:
| T(n, k) = { | 1 | si k=0 |
| n T(n, k-1) + n + 1 | si k>0 |
Se observa que la recurrencia itera en k, pues la siguiente llamada es T(n, k-1) así que podemos ponerla así:
| T(k) = { | 1 | si k=0 |
| n T(k-1) + n + 1 | si k>0 |
Es, por lo tanto, una recurrencia en k y no en n. Apliquemos la técnica del despliegue.
Iteración k:
Iteración k-1:
Iteración k-2:
Iteración k-(k-1)=1:
| = ( 2 ∑j=1..k nj ) + 1 = | 2n(nk-1) | + 1 = |
| n-1 |
| = | 2nk+1-n-1 |
| n-1 |
Por lo tanto
| T(n, k) = | 2nk+1-n-1 |
| n-1 |
Resolver aplicando función generadora
Tomamos la definición que vimos en el apartado anterior:
| T(k) = { | 1 | si k=0 |
| n T(k-1) + n + 1 | si k>0 |
Que podemos expresar así:
Usamo la siguiente función generadora:
Esta es la condición inicial:
Aplicamos la función generadora a la recurrencia [2]:
Resolvemos cada término:
- ∑k≥0 T(k+1) xk = ∑k≥0 T(k+1) xk+1 x-1 =
= 1 ∑k≥0 T(k+1) xk+1 = 1 ∑k≥1 T(k) xk = x x = 1 (- T(0) x0 + ∑k≥0 T(k) xk ) = x = 1 ( G(x) - 1 ) x - n ∑k≥0 T(k) xk = n G(x)
(n+1) ∑k≥0 xk = (n+1) 1 1-x
Agrupamos términos:
| 1 | ( G(x) - 1 ) | = n G(x) + | n+1 | |
| x | 1-x |
Y resolvemos para G(x):
| G(x) = | 1+nx |
| (1-x)(1-nx) |
Descomponemos en fracciones más simples:
| G(x) = | 1+nx | = - | 1 | + | 2 | - | 2x | = |
| (1-x)(1-nx) | 1-x | 1-nx | (1-x)(1-nx) |
| = - | 1 | + | 2 | - | 2 | + | 2 | = |
| 1-x | 1-nx | (1-x)(n-1) | (1-nx)(n-1) |
| = - | n+1 | + | 2n | = |
| (n-1) (1-x) | (n-1) (1-nx) |
| = - | n+1 | × | 1 | + | 2n | × | 1 |
| n-1 | 1-x | n-1 | 1-nx |
Identificamos la serie geométrica
| ∑k≥0 xk = | 1 |
| 1-x |
Y además si hacemos el cambio y=nx entonces 1/(1-nx) = 1/(1-y) que viene a ser también una serie geométrica ∑k≥0 yk = ∑k≥0 (nx)k = ∑k≥0 nk xk:
| ∑k≥0 nk xk = | 1 |
| 1-nx |
Por lo tanto
| G(x) = - | n+1 | × ∑k≥0 xk | + | 2n | × ∑k≥0 nk xk |
| n-1 | n-1 |
Así que el término general es
| T(n, k) = - | n+1 | + | 2n | nk | = | 2nk+1-n-1 |
| n-1 | n-1 | n-1 |
Que es lo mismo que obtuvimos en el apartado anterior
| T(n, k) = | 2nk+1-n-1 |
| n-1 |
Coste con copia de resultados
Como cada resultado parcial tiene una longitud k y hay nk resultados, entonces el coste de copiarlos es k nk. El resultado final con coste de copia queda así:
| T(n, k) = | 2nk+1-n-1 | + k nk |
| n-1 |
Caso con n=1
Posteriormente a publicar este tema detecto que las fórmulas anteriores no contemplan el caso cuando n=1, pues entonces el denominador es cero. Veamos el coste del algoritmo para este caso, cuya recurrencia era como sigue tal como vimos más arriba, recordando que n no variaba en la ejecución:
| T(k) = { | 1 | si k=0 |
| n T(k-1) + n + 1 | si k>0 |
Con n=1 esa recurrencia queda así:
| T(k) = { | 1 | si k=0 |
| T(k-1) + 2 | si k>0 |
Es una recurrencia muy simple, como la que vimos al inicio de esta serie de temas sobre el factorial. De forma compacta es así
y cuya solución, como vemos en WolframAlpha, es:
Entonces nuestras fórmulas deben reescribirse así para contemplar el caso n=1
| n≠1 ⇒ T(n, k) = | 2nk+1-n-1 |
| n-1 |
Y para el caso de coste con copia:
| n≠1 ⇒ T(n, k) = | 2nk+1-n-1 | + k nk |
| n-1 |